Motivation and Context
DeFi lending markets today share two fundamental vulnerabilities: large, discrete supplier exits and hyper-elastic, thin-margin borrower demand fueled by extensive rehypothecation. While these characteristics are common across pools, their combined impact is magnified significantly in whale-dominated and leverage-heavy environments such as ETH, USDT, and USDe.
Under the current piecewise-linear interest rate regime, designed primarily as an ex-post compensation mechanism for suppliers, a sudden large withdrawal causes utilization, defined as borrowed capital B divided by total supplied liquidity S, to spike abruptly toward full utilization. The resultant APR spike theoretically rewards the remaining suppliers and deters full utilization. In practice, however, it often exacerbates the very liquidity stress it aims to prevent, triggering runaway borrower deleveraging and prolonged liquidity locks.
These dynamics can generate severe downstream effects, such as instability in Liquid Staking Tokens (LSTs) and Liquid Restaking Tokens (LRTs), significant stress on stablecoin pegs or redemptions, and ultimately measurable bad-debt risks on the protocol’s balance sheet. The proposed mechanism aims explicitly to neutralize these pathological feedback loops by introducing a time-aware, convex, and bounded interest-rate response, aligning economic incentives in a more robust and predictable manner.
Large Supplier Withdrawals: A Primary Shock Vector
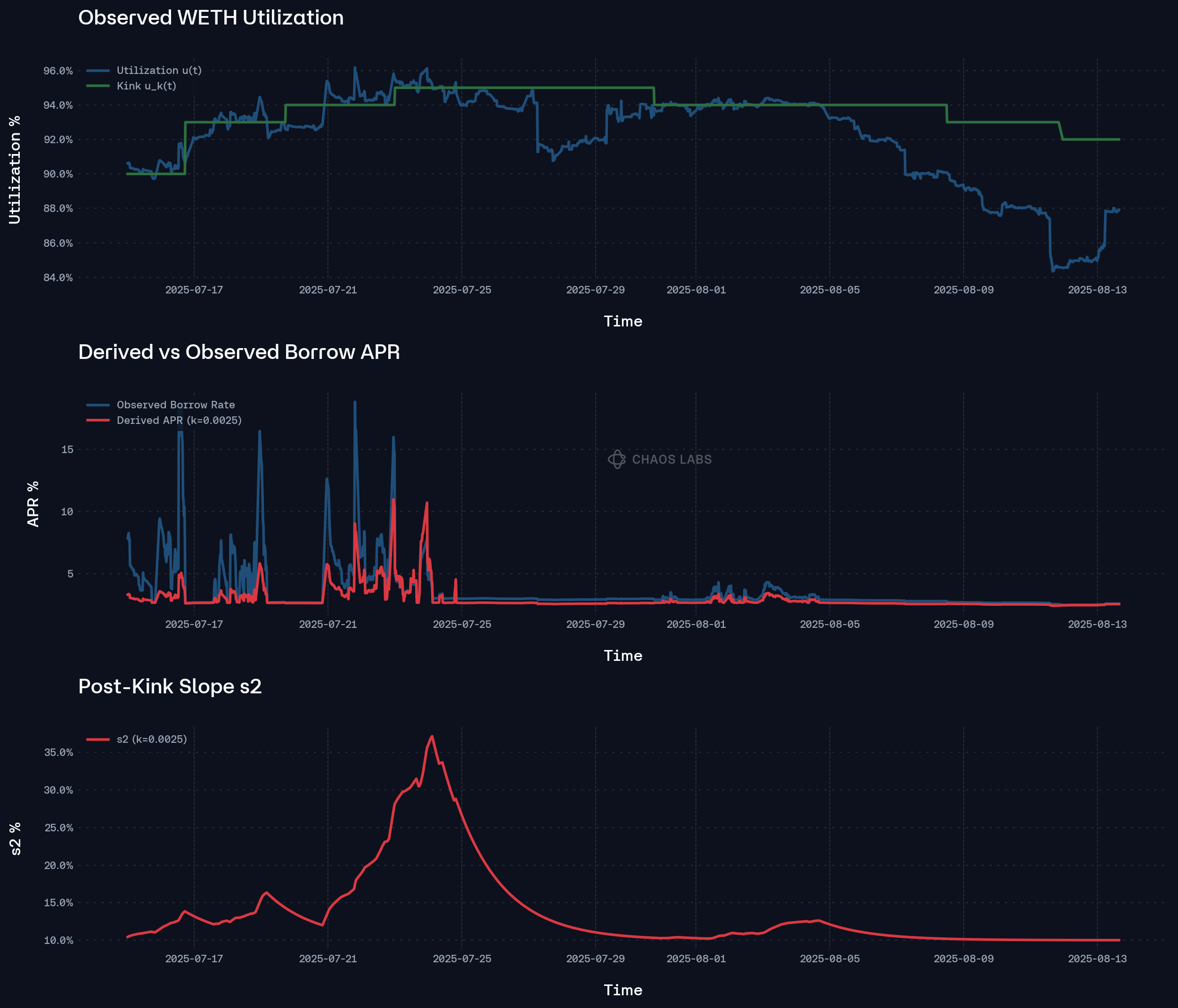
Empirically, the most destabilizing liquidity shocks are not gradual but instantaneous. DAO treasuries, structured products, or whale LPs withdrawing nine- to ten-figure amounts in single-block transactions create immediate and dramatic liquidity shortfalls. This discrete supply reduction causes the utilization ratio to surge abruptly, triggering rapid APR escalations designed to compensate suppliers and attract fresh liquidity.
However, this “supplier-compensation / borrower-disincentive spike” overlooks a core dynamic: the temporal and directional misalignment between supply and demand responses. Elevated APRs may eventually draw in new deposits, but this inflow rarely matches the immediacy of the shock. Meanwhile, the same rate spike acts instantly on borrowers, prompting position unwinds or migration to cheaper venues. In other words, the mechanism compresses supply recovery into a slow path while accelerating demand contraction, worsening liquidity precisely when it is most fragile.
Thin Borrower Margins and Hyper-Elastic Demand Response
This structural issue is amplified by borrower elasticity. Loopers engaging in leveraged carry strategies, particularly prevalent in LST/LRT markets, run at leverage levels of 5–10×, with tail cases exceeding 20×. For these participants, carry margins are razor-thin, often on the order of 20–80 basis points. Even small incremental changes in borrowing APR, in the range of 20–50 basis points, can swiftly render these strategies unprofitable, flipping the economic incentive from positive to negative.
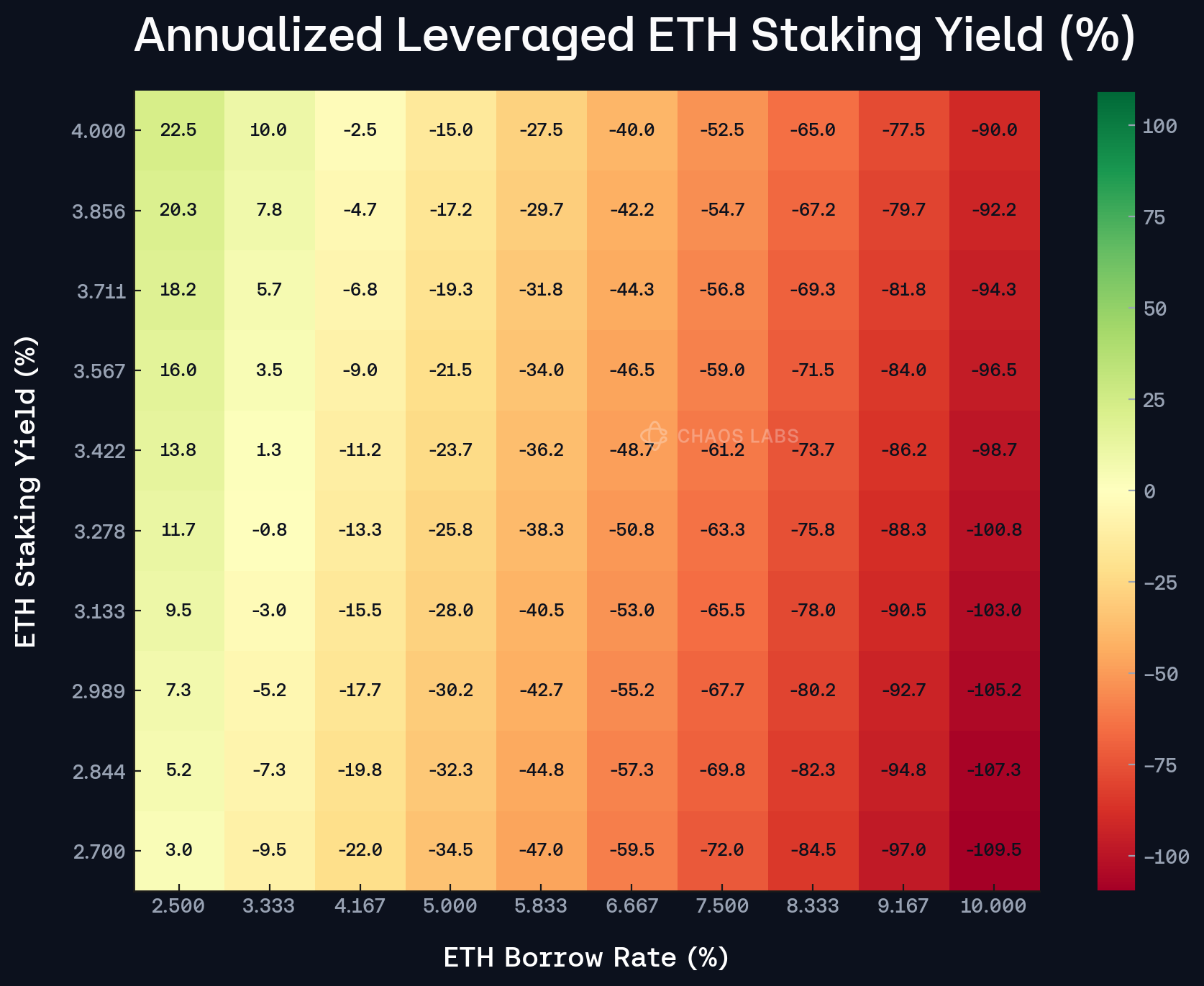
The implications of such an outcome can be observed in the following heatmap, whereby jumps in ETH interest rates ultimately result in significant losses and even hypothetical liquidations stemming from interest accrual (the plot depicts a 15x levered position). As soon as looped positions become unprofitable, each additional minute compounds losses, prompting borrowers to rapidly unwind positions.
Thus, as observed in the chart below, large supplier withdrawals that trigger sharp borrow rate spikes tend not to attract immediate new deposits. Instead, they prompt borrower debt repayments, causing both supply and borrow balances to contract. This synchronized shrinkage amplifies liquidity stress, with second-order effects such as intensified LST and LRT peg pressure and longer delays in the Ethereum exit queue. In parallel with the significant LST and LRT-collateralized stablecoin debt, under the assumption that such an event coincides with a drop in ETH price, can lead to difficulty in offloading such debt positions due to a combination of illiquidity and mispriced collateral eating into the liquidation bonus.
Whale-driven Dynamics and Amplified Risks: USDT and Ethena
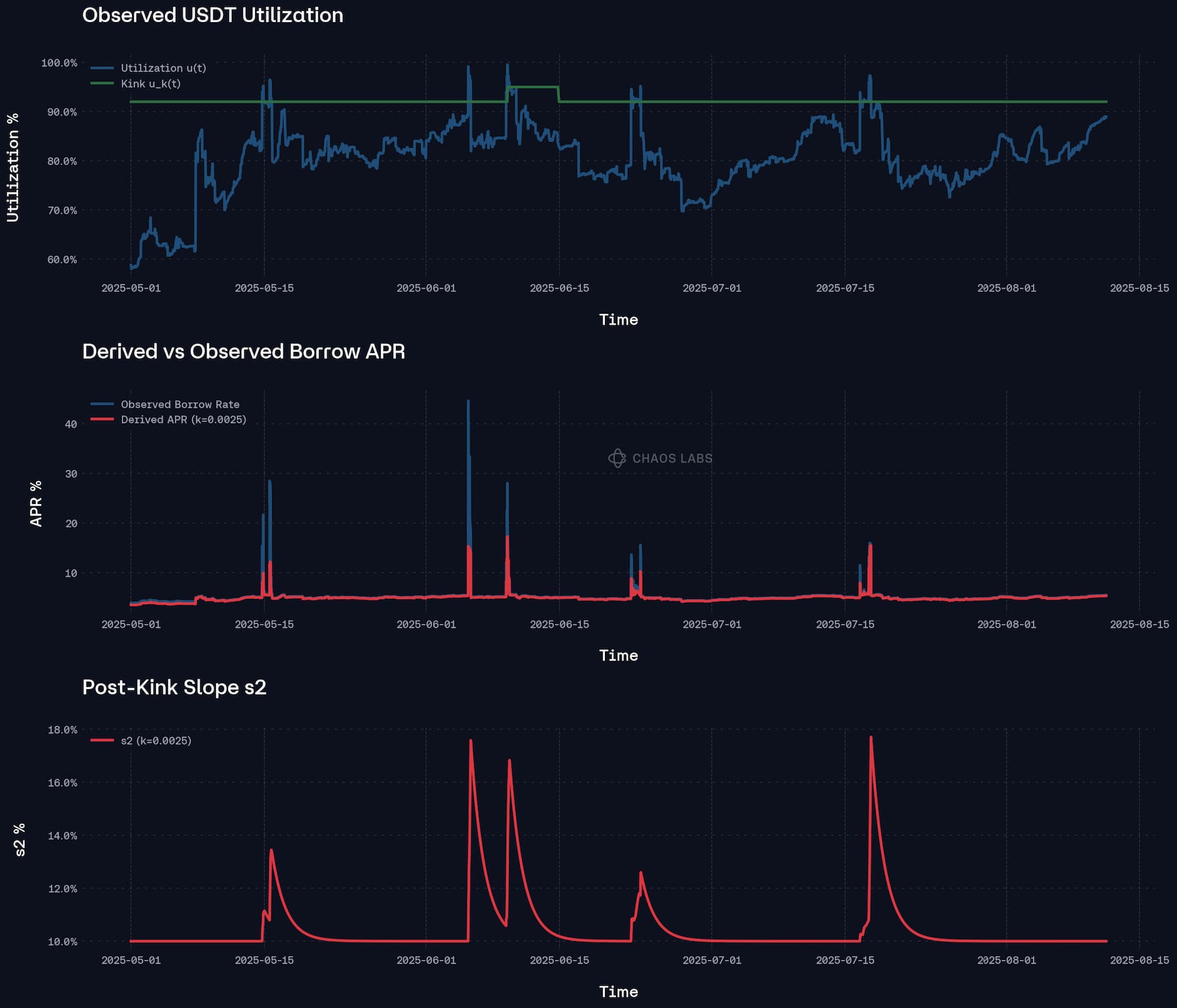
These risks become particularly acute in stablecoin markets like USDT due to significant supplier concentration. For instance, the aUSDT pool is dominated by a small set of super-large entities, including wallets controlled by Justin Sun holding approximately 3.7B aUSDT (45 % of the pool), Ethena hedge wallets holding around 15%, and Plasma pre-deposit vaults holding another 6%. Such extreme concentration means a single whale exit can instantaneously spike utilization, causing drastic rate increases.
In markets with highly concentrated supply, a large depositor can partially withdraw to shrink the denominator, pushing utilization into the steep segment of the rate curve and triggering a sharp, temporary spike in interest rates. By timing such withdrawals, the depositor can keep a smaller residual position that benefits from the elevated rate while freeing capital for other uses, until the market re-equilibrates.
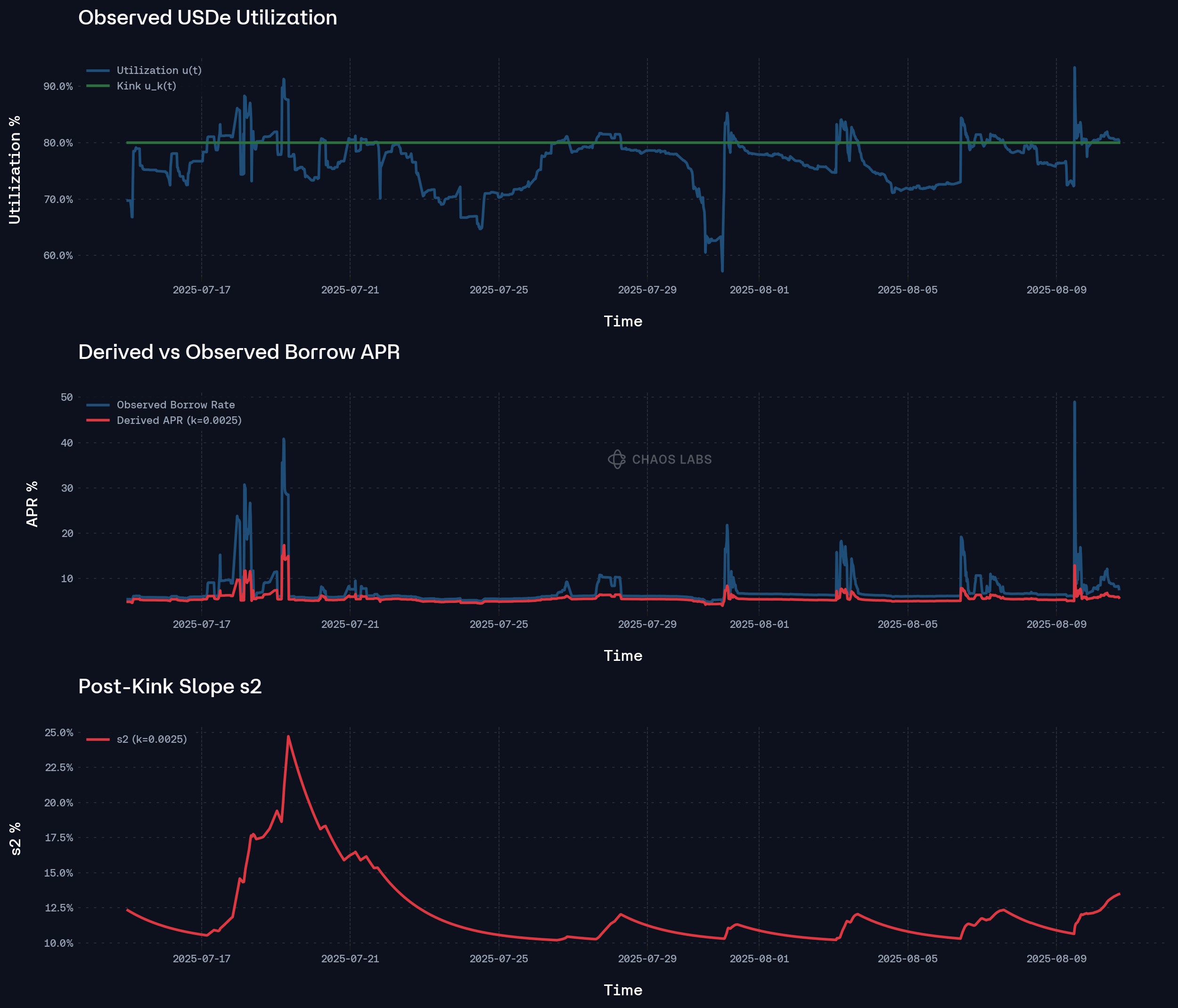
Ethena-denominated strategies compound this further. Ethena-related collateral assets maintain approximately $6B in yield-sensitive looped positions, whose profitability can flip negative under relatively minor rate spikes. In parallel, as a portion of USDe’s USDC and USDT-denominated backing is deposited in Aave aTokens, Ethena’s internal risk framework can stipulate a withdrawal if liquidity shrinks below roughly 1.25× their outstanding hedge exposure, accelerating deleveraging precisely at the peak of liquidity stress. This self-reinforcing cycle can rapidly deteriorate liquidity conditions, causing extended periods of elevated interest rates and widespread instability.
Reflexivity in USDe/sUSDe Markets: Leveraged Supply Meets Leveraged Demand
Similar dynamics are amplified even further in the USDe market due to dual-sided leverage. Liquid Leverage users, consisting of a 50-50 USDe-sUSDe position, generate the full yield of sUSDe while simultaneously rehypothecating base USDe back into lending pools (thereby generating interest). On the flip side, Ethena-denominated PTs leverage the underlying USDe debt to create recursive looping positions to lever into yields and points. As derived via our PT risk oracle, this enables superior capital efficiency and more lenient risk parameterization compared to USDC and USDT as debt assets, as the PTs share the same underlying anchor (USDe), thereby neutralizing fundamental losses in the underlying valuation relative to the debt.
When external yields compress (e.g., sUSDe falls), contraction can initially commence on the USDe supply side, which is posted as collateral to borrow USDT/USDC for looping. As these suppliers unwind, USDe collateral exits, utilization jumps, and borrower costs spike, even if the borrow side remains sticky; PT-collateralized USDe debt rotation into USDT/USDC can follow, but it’s a second-order response to the initial supply withdrawal. (Importantly, in the current iteration of Liquid Leverage, the combination of USDe supplier yield coupled with sUSDe staking yield makes it such that the downside elasticity during sUSDe rate contractions is minimized due to net profitability relative to stablecoin borrow rates via PT borrowing demand generating significant interest)
As outlined rigorously in the research paper “Aave’s Growing Exposure to Ethena: Risk Implications Throughout the Growth and Contraction Cycles of USDe”, such events can lead to substantial interest rate spikes and temporary net looping unprofitability. Effective market stabilization in these scenarios demands active management, leaving slower-acting participants disproportionately harmed due to compounding interest losses over relatively short timeframes.
Conversely, when PT demand surges after a cap increase, rate-agnostic participants will intentionally push USDe borrow rates sharply higher for a short window, expecting external users to close USDe debt or migrate liabilities to USDT/USDC. The result is a deliberate, temporary rate shock that redistributes liquidity but imposes acute costs on slower movers through rapid interest accrual.
A Risk Oracle that Stages the Response
To address these amplified risks systematically, the proposed solution employs a risk oracle designed explicitly around three clearly defined phases, providing a structured, time-aware escalation and recovery path. Instead of one abrupt spike:
-
Initial “Grace” Phase: When utilization crosses the kink, the interest rate increases gradually via a parameterized slope above the kink ($s_2$) in accordance with a minimum viable deterrent. This gentle escalation signals borrowers to unwind positions orderly without inducing panic or simultaneous exits.
-
Escalation Phase: If utilization remains high, slope growth compounds multiplicatively and exponentially. The longer the stress persists, the more expensive it becomes to stay levered. This aligns the mechanism’s “pressure curve” with the borrowers’ own convex cost sensitivity, forcing early deleveraging before liquidity is fully locked.
-
Decay Phase: Once utilization falls below the kink, the elevated slope decays exponentially on a predictable half-life. Borrowers who remain can re-enter at lower rates without facing a sharp reset. Governance does not need to flip switches; decay is automatic.
By embedding a bounded but strictly convex response, this mechanism directly addresses the core solvency risk of prolonged liquidity lockups while preserving fairness for borrowers and safeguarding suppliers through an explicit probabilistic solvency constraint.
Synthesizing the Integrated Rationale
In summary, the necessity of a time-aware, bounded, and convex interest-rate response emerges clearly across all considered lending markets:
-
ETH: Addressing one-sided borrower elasticity amidst sudden large supplier withdrawals.
-
USDT: Mitigating dual-sided reflexivity driven by whale concentration and leveraged hedging exposure, while simultaneously affecting a plethora of yield-generating strategies.
-
USDe: Neutralizing recursive liquidity spirals created by dual-sided leveraged exposure, collateral-debt rotations, and compounded yield sensitivity.
Ultimately, the proposed solution explicitly aligns economic incentives across time and risk dimensions, ensuring market stability, predictable deleveraging paths, and rigorous supplier solvency guarantees across all structurally vulnerable pools.
Design Goals
Engineering an interest-rate mechanism for a highly leveraged DeFi market is fundamentally a problem of shaping dynamic incentives under stress. The curve must (i) induce timely borrower deleveraging before liquidity is exhausted, (ii) guarantee a hard solvency standard for suppliers, and (iii) expose only a minimal, transparent parameter surface to governance. The five goals below articulate these requirements in a formally stated, internally consistent manner.
Convexity Under Stress: Escalating Marginal Penalties
Requirement. For all $u>u_k$, the incremental cost of remaining levered must increase monotonically with both the magnitude of excess utilization and the duration spent above the kink. In discrete time, this is implemented by a multiplicatively compounding post-kink slope such that the effective marginal APR for “one more minute” is strictly larger than for the previous minute, holding u fixed.
Rationale. Prolonged high utilization creates a negative externality: liquidity is rationed and liquidation pathways degrade. A convex penalty schedule internalizes this externality by making delay increasingly expensive, thus shifting individual best responses toward early deleveraging and reducing the expected residence time near full utilization.
Boundedness: Hard Caps, Credible Floors
Requirement. The borrowing rate must be bounded within $[r_{\min}, r_{\max}]$ with $r_{\max}$ chosen as a “pain ceiling” (e.g., 80 % APR) and $r_{\min}$ strictly above the relevant risk-free/staking yield. These bounds are enforced mechanically, not heuristically.
Rationale. Above a certain level, further APR increases do not materially accelerate deleveraging but do induce panic, strategic default, or governance intervention. Conversely, a non-trivial floor prevents the resurgence of recursive carry trades at negligible cost once stress subsides. Boundedness preserves both behavioral credibility (no “infinite APR” fears) and economic discipline.
Memory with Decay: Autonomous Relaxation on a Predictable Half-Life
Requirement. When utilization falls back to or below the kink, the elevated post-kink slope must decay exponentially toward its floor at a governance-specified rate (half-life). No manual reset should be required.
Rationale. A one-way ratchet erodes competitiveness and invites ad hoc overrides; a cliff reset is gameable and induces oscillatory behavior around u_k. Continuous exponential decay ensures that: (i) the system “remembers” stress long enough to deter immediate re-risking, and (ii) borrowers can anticipate precisely how fast costs will normalize, improving planning and trust.
Two-Stage Optimization: Supply Safety First, Borrower Welfare Second
We calibrate the growth and decay parameters (k,λ) through a structured two-step approach designed explicitly to align with the asymmetric economic realities of lending markets:
-
Feasibility filter (supplier solvency): We first apply a stringent feasibility filter that excludes any parameter combinations unable to satisfy a clearly defined probabilistic constraint ensuring supplier solvency. This constraint incorporates collateral price volatility, utilization dynamics, and liquidity duration, rigorously quantifying and bounding the risk of potential bad debt accrual. Parameter choices that fail to meet this solvency standard, validated through extensive simulation and statistical confidence, are strictly discarded.
-
Welfare optimization (borrower & systemic efficiency): Among parameter combinations meeting the solvency criteria, we select those that minimize a comprehensive welfare objective, W(k,λ). This welfare metric penalizes elevated nominal APR levels, representing borrower economic pain, and significant APR variance, reflecting systemic whiplash costs. As a result, borrowers are presented with the most economically efficient rate paths, subject explicitly to the primary constraint of guaranteed supplier safety.
Calibratability: Data-Driven, Reproducible Parameterisation
Requirement. Free parameters (growth k, decay λ, and caps/floors) must be calibrated from empirical telemetry: utilization distributions, stress-episode durations, APR path dynamics, collateral price volatility, and observed liquidation latencies. Recalibration should occur on a periodic cadence via a documented, methodologically consistent process.
Rationale. Market structure is non-stationary: LST liquidity fragments, volatility regimes shift, and looping intensity evolves. Static parameter choices go stale. A well-specified calibration pipeline with recorded inputs and decision criteria reduces discretion, keeps updates principled, and sustains continuity over time.
Synthesis
These goals are mutually reinforcing:
-
Convexity provides the time-critical deleveraging impulse.
-
Boundedness constrains that impulse within socially and behaviorally acceptable limits.
-
Memory with decay creates an algorithmic glide path back to normal conditions with respect to time, creating an approximative feedback loop whereby observed market volatility corresponds with the underlying fixed pricing mechanism at a given time t.
-
Binary safety formalizes supplier protection as a hard feasibility frontier, not a tunable weight.
-
Calibratability ensures the mechanism remains coupled to observed market dynamics and maintains credibility through reproducibility.
Collectively, they define a rate curve that is stringent yet predictable, adaptive yet bounded, and aligned with the asymmetric economics of a recursively levered, liquidity-constrained environment. The intended outcome is rapid stress resolution, minimal post-shock drag, and a statistically guaranteed solvency profile for capital providers.
Disclaimer
Chaos Labs has not been compensated by any third party for publishing this ARFC.
Copyright
Copyright and related rights waived via CC0